UPPER MANTLE SHEAR VELOCITY MODEL

Page content: Model description Acknowledgments References Presentations Interactive plotting tools: Description 1D profile Vertical slice along latitude Vertical slice along longitude Horizontal slice (Orthographic projection) Horizontal slice (Mercator projection) Download model related files Contact information

CUB shear velocity model is created from a large data set of the surface wave fundamental model phase and group velocity measurements. Phase velocities in period range between 40 an 150 s are generously donated by Harvard University and Utrecht University. These phase velocity data sets are described by Ekström et al. (1997) and Trampert and Woodhouse (1995). The group velocity measurements at periods between 16 and 200s are performed at the Center for Imaging the Earth's Interior in the University of Colorado at Boulder. The group velocities are measured with the frequency-time analysis ( Levshin et al., 1989) in which for every waveform a human analyst defines the frequency range of measurements and separate the signal form a variety of noise sources (e.g., overtones, fundamental modes of different types, other earthquakes, multipaths, scattered arrivals). We used broadband waveforms following earthquakes occurred from 1997 to present and recorded at stations from both global networks (GDSN, GSN, GEOSCOPE) as well as temporary regional arrays. At present, the group velocity data-set is composed of about 200000 paths.

Data coverage is generally better for Rayleigh waves than for Love waves, is better at intermediate periods than at very short or very long periods, and is better in the northern than in the southern hemisphere. This heterogeneous data coverage is imposed by the distribution of seismic stations and earthquakes. Data coverage optimizes in Eurasia and is currently worst across Africa, the central Pacific, parts of the Indian Ocean, and Antarctica.

Phase and group velocity of the fundamental mode surface waves are sensitive to the S-wave velocity at depths up to about 200-300 km. Therefore, the measured dispersion curves can be inverted for the distribution of the shear velocity in the crust and upper mantle. The inversion is divided into two steps. The first step is the surface-wave tomography in which the measured dispersion curves are inverted to produce 2-D maps of the geographical distribution of phase and group velocities for individual periods and wave-types. As a result, we estimate at each geographical location four dispersion curves: the phase velocity of Rayleigh and Love waves at periods between 40 and 150 s, and group velocities between 16 s and 200 s period. In the second step, at each geographical location, these four dispersion curves are inverted to obtain a local radially anisotropic 1-D shear-velocity model using a Monte-Carlo method.

Traditionally, the surface wave tomography has been based on the ray theory. Description of the ray-based tomographic method is done by Barmin et al. (2001). However, the ray theory models adequately represents the wave propagation only when the scale of the heterogeneity is larger than the size of the Fresnel zones. Therefore, the ray-based tomography becomes inaccurate to infer a relatively small-scale structure. Recently, we have developed a tomographic method based on a physical model of the surface-wave Fresnel zones and accounts fro associated diffraction effects like the wave-front healing. This diffraction tomography is described by Ritzwoller et al. (2002). At this site, we show two models created with different tomographic methods. The model created with the ray-based and the diffraction tomographies are called CU_SRT1.0 and CU_SDT1.0, respectively.

The details of the Monte-Carlo inversion of the local dispersion curves are described by Shapiro and Ritzwoller (2002). Main idea of this method is to test a large number of randomly generated model realizations and to select those satisfying the acceptance criteria. The result of the inversion process is not a single model but an ensemble of acceptable models that is used to characterize the average model as well as the model uncertainty.

To be able to fit simultaneously the Rayleigh and the Love wave data, we allow our model to be radially anisotropic. Radially anisotropic (transversely isotropic) media is described with five elastic modulus (Dahlen and Tromp, 1998). Surface waves are essentially sensitive to only two of them, i.e., to the S-wave velocities Vsv and Vsh. Therefore, as a result of the Monte-Carlo inversion we estimate the local 1D distributions of these two velocities and their uncertainties. The Monte-Carlo inversion is performed at each of 16020 points of a global 2x2 degree geographical grid and, as a result, a global 3D distribution of shear velocities in the crust and the upper mantle is obtained.

Two tomographic models CU_SRT1.0 and CU_SDT1.0 can be visualized with a set of Interactive plotting tools:

This tool plots a vertical shear velocity profile at a selected geographical point (on 2x2 degree grid). The resulting figure shows the corridors of acceptable values of Vsv and Vsh estimated during the Monte-Carlo inversion. If users selects the "isotropic" option, the average isotropic velocity (Vsv+Vsh)/2 is plotted. The blue line shows the minimal degree of the radial anisotropy required to explain the Rayleigh and Love wave dispersion curves at the considered point.

This tool produces a vertical slices along a latitude selected by the user. Colors shows the perturbation of the average velocity (Vsv+Vsh)/2 relative to the global 1D model AK135 (Kennett et al., 1995). The user can select to plot the location of earthquakes from the EHB (Engdahl et al., 1998) catalog. Black contours delimits the so-called persistent anomalies. An anomaly is considered to be persistent when the velocity perturbation relative to the reference model is larger than the velocity uncertainty. The figure also includes a small map showing location of the selected profile (red line) and the major tectonic plate boundaries (blue lines).

This tool produces a vertical slices along a longitude selected by the user. Colors shows the perturbation of the average velocity (Vsv+Vsh)/2 relative to the global 1D model AK135 (Kennett et al., 1995). The user can select to plot the location of earthquakes from the EHB (Endahl et al., 1998) catalog. Black contours delimits the so-called persistent anomalies. An anomaly is considered to be persistent when the velocity perturbation relative to the reference model is larger than the velocity uncertainty. The figure also includes a small map showing location of the selected profile (red line) and the major tectonic plate boundaries (blue lines).

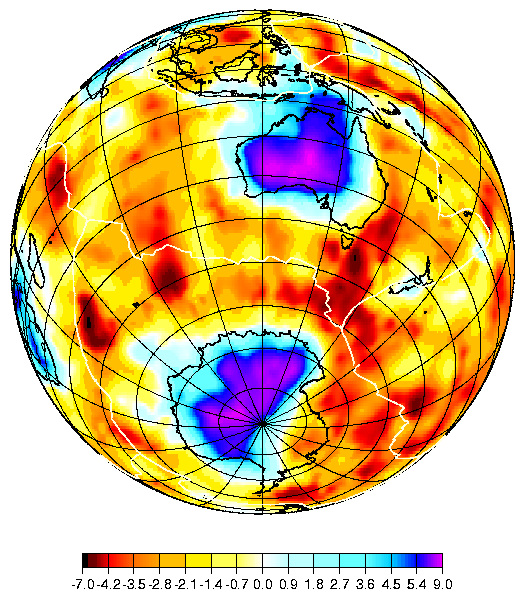
This tool plots the horizontal slice of the model at a selected depth using the orthographic projection with a center selected by the user. Colors show the perturbation of the average velocity (Vsv+Vsh)/2 relative to the average global velocity at the selected depth. This reference velocity is computed from the CUB model and its value is indicated in the figure.

This tool plots the horizontal slice of the model at a selected depth using the Mercator projection in the geographical region selected by the user. Colors show the perturbation of the average velocity (Vsv+Vsh)/2 relative to the average global velocity at the selected depth. This reference velocity is computed from the CUB model and its value is indicated in the figure.

Images of Tibetan crust and upper mantle, Fall AGU 2002.

The model creation has been partially supported by NSF Office of Polar Programs and Defense Threat Reduction Agency. All plotting tools utilize the GMT software.

Barmin, M.P., Ritzwoller, M.H., and Levshin, A.L., A fast an reliable method for surface wave tomography, PAGEOPH, 158, 1351-1375, 2001. (PDF file)

Ritzwoller, M.H., Shapiro, N.M., Levshin, A.L., and Leahy, G.M., Crustal and upper mantle structure beneath Antarctica, J. Geophys. Res., 106, 30645-30670, 2001. (PDF file, Science editors choice)

Ritzwoller, M.H., N.M. Shapiro, M.P. Barmin, and A.L. Levshin, Global surface wave diffraction tomography, J. Geophys. Res., 107(B12), 2335, 2002. (PDF file)

Shapiro, N.M. and M.H. Ritzwoller, Monte-Carlo inversion for a global shear velocity model of the crust and upper mantle, Geophys. J. Int., 151, 88-105, 2002. (PDF file)

Wessel, P., and W.H.F. Smith, Free software helps map and display data, EOS, 72, 441, 1991. (GMT web-page)

Wessel, P., and W.H.F. Smith, New version of the Generic Mapping Tools released, EOS, 76, 329, 1995. (GMT web-page)